Conjugate Beam Method for Real Beam

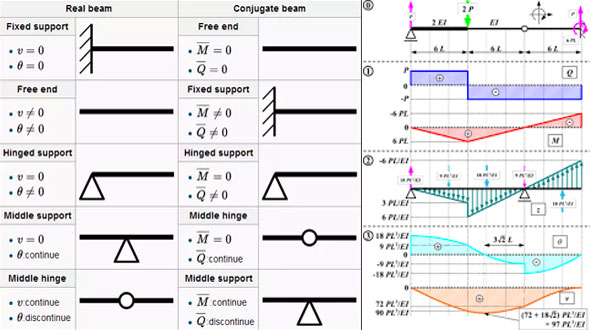
A conjugate beam stands for a fictitious beam with unreal support conditions and unreal loading aimed to get slope and deflection in a real beam.

The conjugate beam method offers several ways to get slopes (rotations) and deflections of determinate beams. It provides the benefits of having equivalent set of relationships which prevail among load(ww)-shear(VV)-moment(MM) and curvature(ϕϕ)-slope(θθ)-deflection(ΔΔ).

Characteristics of Conjugate:

1. The length of a conjugate beam always remains identical to the length of the actual beam.

2. The load on the conjugate beam belongs to the M/EI diagram of the loads on the actual beam.

3. A simple support for the real beam keeps simple support for the conjugate beam.

4. A fixed end for the real beam turns out to be free end for the conjugate beam.

5. The point of zero shear for the conjugate beam serves as a point of zero slope for the real beam.

6. The point of maximum moment for the conjugate beam serves as a point of maximum deflection for the real beam.

Supports of Conjugate Beam:

Understanding that the slope on the real beam is identical to the shear on conjugate beam and the deflection on real beam is identical to the moment on conjugate beam, the shear and bending moment at any point on the conjugate beam should be uniform with the slope and deflection at that point of the real beam.

Also Read: Application of Beam Deflection Formula

As for instance a real beam with fixed support; at the point of fixed support no slope or deflection exist, thus, the shear and moment of the related conjugate beam at that point should be zero. So, the conjugate of fixed support is free end.

To learn how to create a conjugate beam from the given real beam, go through the following video tutorial.

Video Source: Civil Engineering